
When there is a fraction involved, it is easier to take his multiples so we can get whole numbers: When we’re comparing two lines, if their slopes are equal they are parallel, and if they are in a relation $a_1=-\fracx$ If variable $x$ is a constant $x =c$, that will represent a line paralel to $y$-axis. If the slope is equal to number $0$, then the line will be paralel with $x$ – axis. The slope of a line is a number that describes steepness and direction of the line.Ī slope ($a$) is calculated by the formula: The number infront of variable $x$ indicates the slope of your line. Now we have linear function graph which is a line. All you have to do to make a graph is put them in the plane, and connect them with a straight line. In that rule you “put you $x$ to get $f(x)$”. You only need two points to make a line, but for precise in drawings, this time we’ll take three points. This only means that you take x arbitrarily, and your $f(x)$ depends on your choice.Įxample: Draw a graph of linear function: $f(x) = 2x$įirst you have to make your dependant/independant variable table. There are two parts of every linear function, the dependent variable, or $f(x)$ in this case, and independant variable, $x$. For linear functions that graph is a straight line that goes trough the $(0, 0)$ coordinate.
A graph is a set of all ordered pairs that satisfy rule of a function. Every function is represented by a graph. That means that you can take any numbers in the place of $x$ and get yourself an ordered pair of numbers. In this rule, $x$ is the changeable variable. In our examples $f (x)$, placed on the bottom of this lessons, will be replaced with $y$. Linear function is a function given by a rule $ f(x) = a \cdot x$, where $a$ is from $a$ set of real numbers. First number indicates where the point is located considering $x$- axis, and second considering $y$- axis. Their intersection will be marked with point $O$, on the $x$-axis, numbers on the left will be negative and on the right positive, and on $y$-axis, numbers below $0$ will be negative and above positive.Ī coordinate is an ordered pair of numbers which tells us where specific point is located. Vertical is called the $y$-axis, and horizontal $x$-axis. We all know what a number line is, but now we’ll have to go a step further and define a number plane.Ī number plane has two axis, horizontal and vertical. To read more about x-intercepts and y-intercepts, check out the articles Understanding x-intercepts and Understanding y-intercepts.Before we define linear function let’s first define few terms. This gives you two points on the line, which you can plot and then connect to graph the linear equation. Two easy values here would be 0 and 3 (Since the 3 will cancel with the 3 in the fraction.)

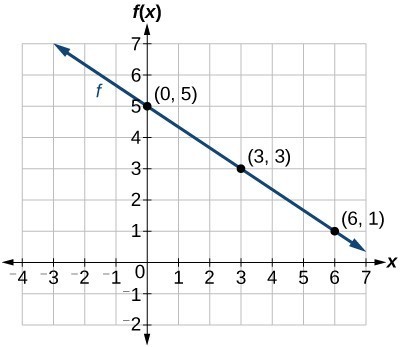
To find two points on the line, pick any two values of \(x\) that would be easy to work with and then find the corresponding value of \(y\). The idea with this method is to find two points on the line by picking values of \(x\). The graph of any linear equation like \(y = 3x + 2\) or \(y = -x + 9\) is a line, and only two points are needed to define a line. Method 1: using two points to graph a linear equation


 0 kommentar(er)
0 kommentar(er)
